Nick Brown's blog: 2024

In my previous blog post I mentioned that the next one, which you are reading now, would look at a recent paper from Nicolas Guéguen that I investigated using a technique that James Heathers and I (mostly me, this time) developed, which we call RIVETS.

RIVETS is a fairly minor part of the data-forensic toolbox. I think it's worth reading the preprint linked above, but then I am biased. However, even if you don't want to get your head around yet another post hoc analysis tool — which, like all such methods has limitations — please keep reading anyway, because the analysis took a "WTF" turn as I was initially about to publish this post. I promise you, it's worth it. If you are in a hurry, skip to the section entitled "A blast from the past", below.

The article

Here is the article that I'll be discussing in this post:

Jacob, C., Guéguen, N., & Delfosse, C. (2024). Oh my darling Clementine: Presence vs absence of fruit leaves on the judgment of a fruit-juice. European Journal of Management and Marketing Studies, 8(4), 199–206. https://doi.org/10.46827/ejmms.v8i4.1712

On 2024-09-06 I was able to download the PDF file from here. (Amusingly, one of the first things that I noticed is that it cites an article from the late Cornell Food and Brand Lab.)

Judging from the appearance of its articles and its website, the journal appears to be from the same stable as the European Journal of Public Health Studies, which published the paper that I discussed last time. So, again, not a top-tier outlet, but as ever, it's what's in the paper that counts.

The subject matter of the article is, as is fairly typical for Guéguen, not especially challenging from a theoretical point of view. 100 participants were assigned to drink a plastic cup of clementine juice while seated at a table with some clementines on it, and then rate the juice on five measures. There were two conditions: In one condition the clementines were just naked fruit, and in the other they still had some leaves attached to them. There were 50 participants in each condition.

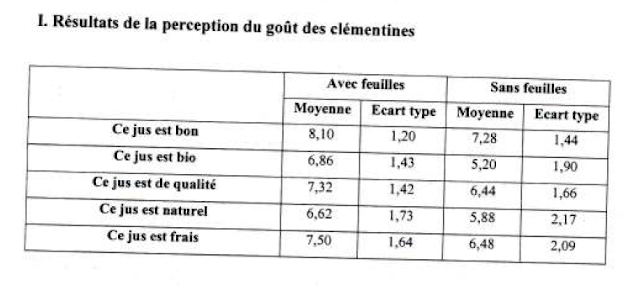
Let's have a look at the results. Here is Table 1:

Four of the results attain a conventional level of statistical significance and one doesn't.

Introducing RIVETS

When I see a table of results like this in a paper that I think might be of forensic interest, my first reaction is to check that they are all GRIM-consistent. And indeed, here, they are. All 10 means pass GRIM and all 10 SDs pass GRIMMER. This is of course a minimum requirement, but it will nevertheless become relevant later.

The next thing I check for is whether the test statistics match the descriptives. There are a couple of ways to do this. These days I generally use some code that I wrote in R, because that lets me build a reproducible script, but you can also reproduce the results of this article using an online calculator for t tests (remember, F = t²) or F tests. Whichever you choose, by putting in the means and SDs, plus group sizes of 50, you should get these results:

You can see that in three of the five cases, the calculated F statistic exactly matches the reported one to 2 decimal places. And in fact when I first did the calculations by hand, I erroneously thought that the published value of the first statistic (for Goodness) was 9.41, and so thought that four out of the five were exact matches.

Why does this matter? Well, because as James and I describe in our RIVETS preprint, it's actually not especially likely that when you recalculate test statistics using rounded descriptives you will get exactly the same test statistic to 2dp. In this case, for the three statistics that do match exactly, my simulations show that this will occur with 5.24%, 10.70%, and 6.73% of possible combinations of rounded input variables, respectively.

Had those been the only three test statistics, we would have a combined probability of all three matching of 0.0003773, which — assuming that the numbers are independent — you can treat roughly as a p value. In other words, it's not very likely that those numbers would appear if they had been produced with real data. And we can go further: If (again, this is not the case) the first two F statistics had been reported as 9.41 and 23.11, the percentages for those in the simulation are 3.93% and 3.00%, so the combined probability of all five matching would be 4.449e-7, which is very unlikely indeed.

But, as we wrote in the RIVETS preprint, the analyst has to be principled in its application. Two of the five reported test statistics were not what we might call "RIVETS-perfect", which seems like quite strong evidence that those numbers were generated from real data (unless, perhaps, the authors took RIVETS into account, in which case, they should take a bow). At this point the forensic analyst has to grimace a bit and go and get a cup of coffee. This line of investigation (i.e., the hypothesis that the authors had no data and merely made up the summary statistics) is probably a dead end.

And that was going to be the end of this post. An interesting forensic near-miss, an illustration of how to use RIVETS in a (hopefully) principled way, but no obvious signs of malfeasance. And then things took an interesting turn...

Another blast from the past

As I was going through the rather extensive tree of directories and files that live on my computer under the top-level directory "Guéguen", looking for the R code to share, I saw a directory called "Clementines". I thought that I had filed the code elsewhere (under "Guéguen\Blog posts\2024", since you ask), but my memory is not great, so maybe I created a folder with that name. I went into it, and here's what I found:

Check out those dates. Apparently I had been looking at a Guéguen(-related) study about clementines way back in 2016. But was it the same one? Let's open that† PDF file and look at the table of results:

These numbers certainly look quite similar to the ones in the article. Six of the means are identical and four (all but the top value in the left-hand column) are slightly different. All of the SDs are similar but slightly different to the published values. Elsewhere in the document, I found the exact same photograph of the experimental setup that appears on p. 202 of the article. This is, without doubt, the same study. But how did I get hold of it?

Well, back in 2016, when the French Psychological Society (SFP) was trying to investigate Guéguen's prolific output of highly implausible studies, he sent them a huge bunch of coursework assignment papers produced by his students, which the SFP forwarded to me. (Briefly: Guéguen teaches introductory statistics, mainly to undergraduates who are majoring in business or economics, and sends his students out in groups of 3 or 4 to collect data to analyse with simple methods, which they often end up faking because doing fieldwork is hard. See this 2019 post for more details on this.)

The pile of student reports sent by Guéguen to the SFP in 2016. None of these answered any of the questions that the SFP had put to him, which were about his published articles. At the time, as far as I know, none of the 25 reports had yet been converted into a published journal article. The French expression "noyer le poisson" comes to mind here.

The above table is taken from one such student assignment report. The analysis is hilarious because the students seem to have fallen asleep during their teacher's presentation of the independent-samples t test and decided that they were going to treat a difference of 0.5 in the means as significant regardless of the standard deviation or sample size. (I guess we could call this the "students' t test", ha ha.)

"In order to determine a meaningful difference between the means that we obtained, we set a threshold of 0.5. On this basis, all the results of the analysis were significant"

Now, for some reason this particular paper out of the 25 must have stood out for me, because even though the analysis method used is hot garbage, back in October of 2016 I had actually tried to reproduce the means and SDs to try to understand the GRIM and GRIMMER inconsistencies. To their great credit, the students included their entire dataset — every observation of every variable — in their report, and it was not difficult to type these numbers into Excel. Here are the last few lines of that spreadsheet. (The first and seventh columns, with all 1s and 0s, are the conditions.)

Compare those means and SDs with the table in the published article. You will see that all 20 values are identical. I'm not sure how the students managed to get so many of their means and SDs wrong. The data in the report are presented in the form of a table that seems to be in a computer file (as opposed to handwritten), but maybe they didn't know how to use Excel to calculate the means and SDs, and attempted to do it manually instead.

Since I apparently also imported the data into an SPSS file back in 2016, it seems that I also probably did some analyses to see what the t test or one-way ANOVA results would give (as opposed to the students' choice to count a mean difference of 0.5 as "significant"). I don't have SPSS any more, but I read the Excel data into R and got these results:

Item	F statistic
Bon	9.44
Bio	23.14
Qualité	7.46
Naturel	2.98
Frais	6.63

You can see that these match the published article exactly. This strongly suggests that the authors also typed in the data from the students' report (or, perhaps, had access to an original file of that report). It also means that my decision to not call the "p = .0003773" RIVETS result suspicious was the right one, because the claim with RIVETS is that "these results were not produced by analysing raw data", and right here is the proof of the opposite.

Comparing the students' report with the published article

I have translated the students' report into English and presented it, paragraph by paragraph next to the French original, in this file [PDF]. I encourage you to read it and compare it with the published article. Several discrepancies between the methods sections of the two documents are evident, such as:

The article states that participants were "welcomed by a research assistant and invited to enter a room". In contrast, the students' report states that the experiment was conducted directly in the hall of the Lorient University Institute of Technology, where they recruited participants by intercepting people as they passed by and invited them to come to a table, with no mention of a separate room.
The article reports that the clementine juice was served at a temperature of 6°C. The students' report does not discuss the temperature, and it does not seem that the students took any particular precautions to serve the juice at a controlled temperature. The photographs show the juice in a clear plastic or glass bottle that does not appear to have any sort of thermal insulation, nor does it seem likely that a refrigerator would be available in the hall (or that the students would have failed to mention this degree of investment in maintaining a constant temperature if they had made it).
The article mentions that participants were debriefed and asked if they thought they knew what the purpose of the experiment was. Nothing of this kind is mentioned in the students' report.
The article says that the participants were "100 Caucasian undergraduate science students at the University of Bretagne-Sud in France". It does not mention their sex breakdown or age range. The students' report states merely that participants were people who were encountered at the Lorient University Institute of Technology (which is indeed a part of the University of Bretagne-Sud), with an unknown academic status, overwhelmingly male, and with an age range of approximately 17 to 60, which suggests that at least some were not undergraduates. Additionally, the students did not report the race of the participants, which would in itself be an extremely unusual data point to collect in France. Anecdotally, it is quite likely that several of them would not be "Caucasian" (a totally meaningless term in French research circles).

I think it it is an open question whether the results reported in the article (and by the students, once their summary statistics are corrected to match their raw data) are genuine. The students' description of the study, which again I strongly encourage you to read, does not sound to me like a description of an experiment that never took place; there are some real human touches and details that seem unlikely to have been invented. However, some patterns in the results are curious. For example, although the five questions that were asked of participants ostensibly measured different aspects of their perception of the juice, the overall Cronbach's alpha for the whole sample is 0.885, and for the two conditions it is 0.782 (with leaves) and 0.916 (no leaves) — results that a psychologist who was trying to design a "Juice Quality Evaluation Scale" would probably be very happy indeed to discover. Also, it is noticeable that (a) only 18 responses of 10 were given out of 500, with only 14 people giving one or more responses of 10; (b) none of the 100 participants responded with the same value for every item; and (c) 61 of the participants did not give the same value to more than two items. One might expect a greater amount of identical responses within participants to such a "light" questionnaire, especially since the overall consistency is so high. However, trying to establish whether the results are real is not my main focus at this point.

Why are the students not credited?

The main question is why the four women‡ undergraduates who devised, carried out, and wrote up the experiment are not credited or acknowledged anywhere in the Jacob et al. article, which does not mention anyone else apart from the authors, other than "a research assistant". We know that the study was performed (or at least written up) no earlier than 2013, when the last of the articles in the References section was published, and no later than 2016, when the collection of student reports was sent to the SFP. Of the three authors of the article, Jacob and Guéguen are senior academics who were both publishing over 20 years ago, and Delfosse's LinkedIn page says that she obtained a Masters degree in Marketing in 2002 and has been a lecturer at the Université de Bretagne-Sud since 2010, so she is also not one of the undergraduates who were involved.

These four undergraduates deserve to be the principal authors of the article, perhaps with their teacher as senior author. This assignment will have received a mark and there will be a trace of that, along with their names, in the university's records. Even if it proved to be impossible to contact all four (former) students, they could have been acknowledged, perhaps anonymously. But there is absolutely nothing of that kind in the article. Quite simply, this study seems to have been stolen from the students who conducted it. If so, this would not be the first time that such a thing seems to have happened in this department.

Conclusion

Writing this post has been a bit of a wild ride. I was originally intending to write it up as an example of how RIVETS can't always be used. The presence of one value that is not RIVETS-perfect (among four that are) ought to bring an investigation based solely on the test statistics to a halt, and that was what I was planning to write. But then I discovered the old student assignment, and I have to confess that I spend a good couple of minutes laughing my head off. I guess the moral here is "never delete anything", and indeed "never throw anything away". But that way lies madness (and indeed a desperate lack of space in your basement), so it seems I was just very lucky to have (a) looked at the student report back in 2016, and (b) stumbled upon it in my file system all these years later.

Supporting information

You can download the relevant documents, code, and data for this post from here.

Footnotes

† Back in 2016 I had apparently only scanned two pages of the student report, without unstapling it, hence the slightly skewed angle of the table. I have now removed the staple and scanned all 17 pages of the report, in a PDF that you can find in the supporting information. There are a few handwritten annotations, which I made in 2016.

‡ The number and gender of the students is revealed in the report, either explicitly (for the number) or implicitly (for the gender, by the fact that all of the adjectives that describe the students are in the feminine form, which in French implies that everyone in the group to which the adjective refers was female).