From the GRIM archive: Eskine et al. (2011)

Readers who have followed the development of GRIM might recall that we (that's me and the Wild Man of Boston) asked 21 researchers for their data. We got nine datasets, and the responses from the other 12 varied between silence and borderline hostility—in two cases, which shared no co-authors, identically-worded borderline hostility.

However, one of the most surprising responses was not a response at all; our e-mail to the lead and corresponding author bounced. Undeliverable. Address not found.

Not so unusual, you might think; after all, people move to new institutions, and their faculty e-mail addresses often evaporate shortly after. But in this case, it was the author's Gmail address that had stopped working.

Spooky

Do I have your attention? Then let's begin...

The article

This is the article that attracted our attention:

Eskine, K. J., Kacinik, N. A., & Prinz, J. J. (2011). A bad taste in the mouth: Gustatory disgust influences moral judgment. Psychological Science, 22(3), 295–299. https://doi.org/10.1177/0956797611398497

On 2025-02-13 I was able to download the PDF file from here. By that point it had acquired 675 citations on Google Scholar and 267 on Web of Science, which seems like quite a lot.

Briefly, the article describes a study that investigated whether giving people a small amount of something pleasant or unpleasant to drink also made them more or less harsh in their judgment of moral transgressions that they read about in a series of vignettes (e.g., second cousins having sex, or someone eating their already-dead dog). There were three conditions, depending on which beverage the participants consumed: Bitter, Sweet, or Water (with the latter condition sometimes being referred to as "control" in the article). For added fun, and because this was back before the tsunami hit social psychology and it was absolutely standard for any article to have a gratuitous pop at (U.S.) conservatives, there was a test to see whether conservatives were more susceptible to the effects than liberals.

I'll let you guess the results, but yeah, you're right. People who were drinking the bitter beverage became more, well, bitter in their judgments of the various transgressions, and the conservatives even more so. Or as the authors put it, "Taken together, these results suggest that physical disgust helps instantiate moral disgust, and that these effects are more salient in individuals with politically conservative views than in individuals with politically liberal views."

We flagged up this article because it has several GRIM inconsistencies in Table 1.

The article reports (p. 296) that "An overall moral-judgment score was obtained for each of the ... participants (bitter condition: n = 15; sweet condition: n = 18; control condition: n = 21)". But the highlighted numbers are not consistent with those sample sizes. For example, for "Bitter taste"/"Sweet drink", 1.76 * 18 = 31.68, so the nearest possible integer—corresponding to the sum of the participants' ratings—is 32. But 32 / 18 = 1.7777 which should be reported as 1.78. And so on.

The combination of seven GRIM problems out of 12 means, plus the effect sizes, made us want to look at the dataset. But as already mentioned, the lead author had deleted his Gmail and apparently gone off the grid. I contacted one of the co-authors of the article but she did not know where Kendall Eskine or the data might be found, and his most recent employer (Loyola University) told me that he had quit without leaving a forwarding address.

However, a few months later, James and I were discussing this particular article with a colleague, who — as it turned out — had been looking at Eskine's work for some time, and had managed to persuade him to share some datasets, including the one for this article. It was in SPSS format, but it was easy enough for me to convert it to CSV and then analyse it in R.

I was able to reproduce all of the results perfectly, apart from the two "contrasts" mentioned in the last paragraph of the Results section. In that case the means and SDs are all fine, but if I do a simple t test the t value is off slightly and the DFs are 1 more than what is reported, and I don't see how to get those numbers with ANOVA contrasts either. If anyone can help with this I'd be most grateful.

The GRIM issue turns out to be a fairly innocuous mix-up in the reporting of the sample sizes, with the Sweet condition actually having 21 participants and the Water (control) condition having 18, rather than the other way round as reported in the article. Going back to the first number in the Sweet column: 1.76 * 21 = 36.96; the nearest integer is 37; 37 / 21 = 1.7619 which rounds to 1.76; and so on.

So, the dataset matches the results and there are no GRIM problems once you fix a typo. Can we go now? (Of course not. Spoiler: this is a blog post, and it has a point to make.)

Looking at the dataset, it seems that participants were asked two items about each of the six vignettes, rather than just one.

The naming of the variables is a little haphazard at points, but we can see that for every vignette ("Incest", "Eatingdog", etc) there are two variables, one measuring how (im)moral the participant considered the behaviour to be, and the other apparently measuring how "appalling" they found it. However, there is absolutely mention of the second set of measurements anywhere in the article (try it: you won't find the string "appal" anywhere in the PDF).

It is tempting to imagine that the authors omitted^† to report the results (or even the existence) of the "appalling" measure because these were not statistically significant. For example, the main effect of beverage that underpins the results, which for the "moral" items was F(2,51)=7.368, p=.002, η_p²=.224, only gives F(2,51)=2.511, p=.091, η_p²=.090 for the "appalling" items, and the other results are similarly unimpressive. The manuscript was submitted is 2010, and back then you weren't going to get into Psychological Science with p=.091.

Another noteworthy thing is that the effect sizes are huge. By consuming just two teaspoons of a bitter, sweet, or neutral-tasting beverage, participants' responses came to differ by over one standard deviation. Again, this was all considered entirely plausible in 2010. Furthermore, the sample sizes are small, and for the conservative–liberal contrasts they are tiny, with just 6 conservatives and 7 liberals in the Bitter condition.

Now, there is rarely any mystery about where effects like these are coming from in the data. It's either a very large difference in means, or very small standard deviations (leading to small standard errors and hence a larger t ratio)—unless you have a huge sample size, in which case that on its own will give you a small SE. Very small SDs are often a sign of problems, especially if they are associated with means in the middle of the range of possible values, as this suggests that almost everyone was answering in the same "non-extreme" way, which doesn't often happen. Looking at the numbers here, however, the SDs appear reasonable, given the authors' claim of a large effect. Put another way, if there really was a true large effect—which is always possible^‡—these are something like the SDs that we would expect to see, including the fact that they are smaller for the larger means as the latter approach the limits of the 0–100 rating scale. The effect is thus being driven principally by the difference in the means across the two groups.

So what else can we look at? Well, let's think about what the authors were measuring. They asked participants about two attitudes ("Is it (im)moral?" and "Is it appalling?") to six transgressions. While they didn't claim to be setting out to make a six-item "Transgression Judgement Scale", and they did not average the response scores across the six vignettes, we might reasonably expect that people who found any one of them to be immoral/appalling might also have a similar opinion about the others. We can measure the extent to which the authors created an internally consistent measure of people's attitudes to these transgressions by examining the Cronbach's alpha values of each measure in each condition. 

Here are the alphas for the two attitudes and the three conditions:

As you can see, for the Bitter condition, the reliability of the measure is considerably less robust, even though the manipulation is meant to be making people more attuned to moral issues, or more readily appalled, than those sampling the more usual beverages.

Let's see what happens when we compute the alphas after breaking the sample down further by political orientation:

Did you even know that Cronbach's alpha can be negative? Well, it can, and it's a useful test of a scale that has reverse-scored items — if you forget to do the reversing, you can end up with a negative alpha. But here, those bitter ol' conservatives are answering the same questions as everyone else. They've just been driven so gosh-darn mad by this appalling immorality that they have no idea what they're doing any more. Or... perhaps something else happened to the data, especially in the bitter condition, and especially for conservatives. <miss_piggy_flutters_eyelashes.gif>

Either way, these results tell us very little about what the experiment was supposed to measure. If anyone has an e-mail address for the lead author that still works, perhaps they could send him a pointer to this post and see if he has an explanation for all this.

Supporting information

I have made the R code and dataset for this post, as well as my annotated copy of the article PDF file, available here.

Footnotes

^† Unless, of course, the reviewers or editors told the authors to "simplify" the story. Simmons et al.'s classic "False-Positive Psychology" article did not land on the editor-in-chief's desk at Psychological Science for another four months after Eskine et al.'s article was published.

^‡ I try, not always successfully, to avoid pointing and laughing at studies purely for having large effect sizes. If we dismiss the possibility of large effects a priori, while also dismissing very small effects as being probably due to noise or unmeasured confounding (and in any case probably not of practical interest), we risk declaring that science is only about "Goldilocks"-sized effects. I don't know what the effect size of penicillin on staphylococcus was back in the late 1920s, but I suspect that it might cause eyebrows to be raised if Alexander Fleming were to write it up for publication today. That said, I remain skeptical of all effect sizes in social psychology above about d=0.4 that were not written about by Plato or Shakespeare.

The return of Nicolas Guéguen, part deux: RIVETS and steal

In my previous blog post I mentioned that the next one, which you are reading now, would look at a recent paper from Nicolas Guéguen that I investigated using a technique that James Heathers and I (mostly me, this time) developed, which we call RIVETS.

RIVETS is a fairly minor part of the data-forensic toolbox. I think it's worth reading the preprint linked above, but then I am biased. However, even if you don't want to get your head around yet another post hoc analysis tool — which, like all such methods has limitations — please keep reading anyway, because the analysis took a "WTF" turn as I was initially about to publish this post. I promise you, it's worth it. If you are in a hurry, skip to the section entitled "A blast from the past", below.

The article

Here is the article that I'll be discussing in this post:

Jacob, C., Guéguen, N., & Delfosse, C. (2024). Oh my darling Clementine: Presence vs absence of fruit leaves on the judgment of a fruit-juice. European Journal of Management and Marketing Studies, 8(4), 199–206. https://doi.org/10.46827/ejmms.v8i4.1712

On 2024-09-06 I was able to download the PDF file from here. (Amusingly, one of the first things that I noticed is that it cites an article from the late Cornell Food and Brand Lab.)

Judging from the appearance of its articles and its website, the journal appears to be from the same stable as the European Journal of Public Health Studies, which published the paper that I discussed last time. So, again, not a top-tier outlet, but as ever, it's what's in the paper that counts.

The subject matter of the article is, as is fairly typical for Guéguen, not especially challenging from a theoretical point of view. 100 participants were assigned to drink a plastic cup of clementine juice while seated at a table with some clementines on it, and then rate the juice on five measures. There were two conditions: In one condition the clementines were just naked fruit, and in the other they still had some leaves attached to them. There were 50 participants in each condition.

Let's have a look at the results. Here is Table 1:

Four of the results attain a conventional level of statistical significance and one doesn't.

Introducing RIVETS

When I see a table of results like this in a paper that I think might be of forensic interest, my first reaction is to check that they are all GRIM-consistent. And indeed, here, they are. All 10 means pass GRIM and all 10 SDs pass GRIMMER. This is of course a minimum requirement, but it will nevertheless become relevant later.

The next thing I check for is whether the test statistics match the descriptives. There are a couple of ways to do this. These days I generally use some code that I wrote in R, because that lets me build a reproducible script, but you can also reproduce the results of this article using an online calculator for t tests (remember, F = t²) or F tests. Whichever you choose, by putting in the means and SDs, plus group sizes of 50, you should get these results:

You can see that in three of the five cases, the calculated F statistic exactly matches the reported one to 2 decimal places. And in fact when I first did the calculations by hand, I erroneously thought that the published value of the first statistic (for Goodness) was 9.41, and so thought that four out of the five were exact matches.

Why does this matter? Well, because as James and I describe in our RIVETS preprint, it's actually not especially likely that when you recalculate test statistics using rounded descriptives you will get exactly the same test statistic to 2dp. In this case, for the three statistics that do match exactly, my simulations show that this will occur with 5.24%, 10.70%, and 6.73% of possible combinations of rounded input variables, respectively.

Had those been the only three test statistics, we would have a combined probability of all three matching of 0.0003773, which — assuming that the numbers are independent — you can treat roughly as a p value. In other words, it's not very likely that those numbers would appear if they had been produced with real data. And we can go further: If (again, this is not the case) the first two F statistics had been reported as 9.41 and 23.11, the percentages for those in the simulation are 3.93% and 3.00%, so the combined probability of all five matching would be 4.449e-7, which is very unlikely indeed.

But, as we wrote in the RIVETS preprint, the analyst has to be principled in its application. Two of the five reported test statistics were not what we might call "RIVETS-perfect", which seems like quite strong evidence that those numbers were generated from real data (unless, perhaps, the authors took RIVETS into account, in which case, they should take a bow). At this point the forensic analyst has to grimace a bit and go and get a cup of coffee. This line of investigation (i.e., the hypothesis that the authors had no data and merely made up the summary statistics) is probably a dead end.

And that was going to be the end of this post. An interesting forensic near-miss, an illustration of how to use RIVETS in a (hopefully) principled way, but no obvious signs of malfeasance. And then things took an interesting turn...

Another blast from the past

As I was going through the rather extensive tree of directories and files that live on my computer under the top-level directory "Guéguen", looking for the R code to share, I saw a directory called "Clementines". I thought that I had filed the code elsewhere (under "Guéguen\Blog posts\2024", since you ask), but my memory is not great, so maybe I created a folder with that name. I went into it, and here's what I found:

Check out those dates. Apparently I had been looking at a Guéguen(-related) study about clementines way back in 2016. But was it the same one? Let's open that† PDF file and look at the table of results:

These numbers certainly look quite similar to the ones in the article. Six of the means are identical and four (all but the top value in the left-hand column) are slightly different. All of the SDs are similar but slightly different to the published values. Elsewhere in the document, I found the exact same photograph of the experimental setup that appears on p. 202 of the article. This is, without doubt, the same study. But how did I get hold of it?

Well, back in 2016, when the French Psychological Society (SFP) was trying to investigate Guéguen's prolific output of highly implausible studies, he sent them a huge bunch of coursework assignment papers produced by his students, which the SFP forwarded to me. (Briefly: Guéguen teaches introductory statistics, mainly to undergraduates who are majoring in business or economics, and sends his students out in groups of 3 or 4 to collect data to analyse with simple methods, which they often end up faking because doing fieldwork is hard. See this 2019 post for more details on this.)

The pile of student reports sent by Guéguen to the SFP in 2016. None of these answered any of the questions that the SFP had put to him, which were about his published articles. At the time, as far as I know, none of the 25 reports had yet been converted into a published journal article. The French expression "noyer le poisson" comes to mind here.

The above table is taken from one such student assignment report. The analysis is hilarious because the students seem to have fallen asleep during their teacher's presentation of the independent-samples t test and decided that they were going to treat a difference of 0.5 in the means as significant regardless of the standard deviation or sample size. (I guess we could call this the "students' t test", ha ha.)

"In order to determine a meaningful difference between the means that we obtained, we set a threshold of 0.5. On this basis, all the results of the analysis were significant"

Now, for some reason this particular paper out of the 25 must have stood out for me, because even though the analysis method used is hot garbage, back in October of 2016 I had actually tried to reproduce the means and SDs to try to understand the GRIM and GRIMMER inconsistencies. To their great credit, the students included their entire dataset — every observation of every variable — in their report, and it was not difficult to type these numbers into Excel. Here are the last few lines of that spreadsheet. (The first and seventh columns, with all 1s and 0s, are the conditions.)

Compare those means and SDs with the table in the published article. You will see that all 20 values are identical. I'm not sure how the students managed to get so many of their means and SDs wrong. The data in the report are presented in the form of a table that seems to be in a computer file (as opposed to handwritten), but maybe they didn't know how to use Excel to calculate the means and SDs, and attempted to do it manually instead.

Since I apparently also imported the data into an SPSS file back in 2016, it seems that I also probably did some analyses to see what the t test or one-way ANOVA results would give (as opposed to the students' choice to count a mean difference of 0.5 as "significant"). I don't have SPSS any more, but I read the Excel data into R and got these results:

Item	F statistic
Bon	9.44
Bio	23.14
Qualité	7.46
Naturel	2.98
Frais	6.63

You can see that these match the published article exactly. This strongly suggests that the authors also typed in the data from the students' report (or, perhaps, had access to an original file of that report). It also means that my decision to not call the "p = .0003773" RIVETS result suspicious was the right one, because the claim with RIVETS is that "these results were not produced by analysing raw data", and right here is the proof of the opposite.

Comparing the students' report with the published article

I have translated the students' report into English and presented it, paragraph by paragraph next to the French original, in this file [PDF]. I encourage you to read it and compare it with the published article. Several discrepancies between the methods sections of the two documents are evident, such as:

1. The article states that participants were "welcomed by a research assistant and invited to enter a room". In contrast, the students' report states that the experiment was conducted directly in the hall of the Lorient University Institute of Technology, where they recruited participants by intercepting people as they passed by and invited them to come to a table, with no mention of a separate room.
2. The article reports that the clementine juice was served at a temperature of 6°C. The students' report does not discuss the temperature, and it does not seem that the students took any particular precautions to serve the juice at a controlled temperature. The photographs show the juice in a clear plastic or glass bottle that does not appear to have any sort of thermal insulation, nor does it seem likely that a refrigerator would be available in the hall (or that the students would have failed to mention this degree of investment in maintaining a constant temperature if they had made it).
3. The article mentions that participants were debriefed and asked if they thought they knew what the purpose of the experiment was. Nothing of this kind is mentioned in the students' report.
4. The article says that the participants were "100 Caucasian undergraduate science students at the University of Bretagne-Sud in France". It does not mention their sex breakdown or age range. The students' report states merely that participants were people who were encountered at the Lorient University Institute of Technology (which is indeed a part of the University of Bretagne-Sud), with an unknown academic status, overwhelmingly male, and with an age range of approximately 17 to 60, which suggests that at least some were not undergraduates. Additionally, the students did not report the race of the participants, which would in itself be an extremely unusual data point to collect in France. Anecdotally, it is quite likely that several of them would not be "Caucasian" (a totally meaningless term in French research circles).

I think it it is an open question whether the results reported in the article (and by the students, once their summary statistics are corrected to match their raw data) are genuine. The students' description of the study, which again I strongly encourage you to read, does not sound to me like a description of an experiment that never took place; there are some real human touches and details that seem unlikely to have been invented. However, some patterns in the results are curious. For example, although the five questions that were asked of participants ostensibly measured different aspects of their perception of the juice, the overall Cronbach's alpha for the whole sample is 0.885, and for the two conditions it is 0.782 (with leaves) and 0.916 (no leaves) — results that a psychologist who was trying to design a "Juice Quality Evaluation Scale" would probably be very happy indeed to discover. Also, it is noticeable that (a) only 18 responses of 10 were given out of 500, with only 14 people giving one or more responses of 10; (b) none of the 100 participants responded with the same value for every item; and (c) 61 of the participants did not give the same value to more than two items. One might expect a greater amount of identical responses within participants to such a "light" questionnaire, especially since the overall consistency is so high. However, trying to establish whether the results are real is not my main focus at this point.

Why are the students not credited?

The main question is why the four women‡ undergraduates who devised, carried out, and wrote up the experiment are not credited or acknowledged anywhere in the Jacob et al. article, which does not mention anyone else apart from the authors, other than "a research assistant". We know that the study was performed (or at least written up) no earlier than 2013, when the last of the articles in the References section was published, and no later than 2016, when the collection of student reports was sent to the SFP. Of the three authors of the article, Jacob and Guéguen are senior academics who were both publishing over 20 years ago, and Delfosse's LinkedIn page says that she obtained a Masters degree in Marketing in 2002 and has been a lecturer at the Université de Bretagne-Sud since 2010, so she is also not one of the undergraduates who were involved.

These four undergraduates deserve to be the principal authors of the article, perhaps with their teacher as senior author. This assignment will have received a mark and there will be a trace of that, along with their names, in the university's records. Even if it proved to be impossible to contact all four (former) students, they could have been acknowledged, perhaps anonymously. But there is absolutely nothing of that kind in the article. Quite simply, this study seems to have been stolen from the students who conducted it. If so, this would not be the first time that such a thing seems to have happened in this department.

Conclusion

Writing this post has been a bit of a wild ride. I was originally intending to write it up as an example of how RIVETS can't always be used. The presence of one value that is not RIVETS-perfect (among four that are) ought to bring an investigation based solely on the test statistics to a halt, and that was what I was planning to write. But then I discovered the old student assignment, and I have to confess that I spend a good couple of minutes laughing my head off. I guess the moral here is "never delete anything", and indeed "never throw anything away". But that way lies madness (and indeed a desperate lack of space in your basement), so it seems I was just very lucky to have (a) looked at the student report back in 2016, and (b) stumbled upon it in my file system all these years later.

Supporting information

You can download the relevant documents, code, and data for this post from here.

Footnotes

† Back in 2016 I had apparently only scanned two pages of the student report, without unstapling it, hence the slightly skewed angle of the table. I have now removed the staple and scanned all 17 pages of the report, in a PDF that you can find in the supporting information. There are a few handwritten annotations, which I made in 2016.

‡ The number and gender of the students is revealed in the report, either explicitly (for the number) or implicitly (for the gender, by the fact that all of the adjectives that describe the students are in the feminine form, which in French implies that everyone in the group to which the adjective refers was female).

A blast from the past: The return of Nicolas Guéguen

Loyal readers of this blog may have been wondering if there have been any updates on the Nicolas Guéguen story since I wrote this post back in June 2020. Well, actually there have!

First, in April 2022 an Expression of Concern was issued regarding the article that I discussed in this open letter, which was the first paper by Guéguen that I ever looked at. Of course, issuing an EOC — which is still in place over two years later and will probably last until the heat death of the universe — is completely absurd, given that we have smoking-gun level evidence of fraud in this case, but I suppose we have to be grateful for small mercies in this business. Guéguen now has 3 retractions and 10 expressions of concern. Hallelujah, I guess.

Second, after a hiatus of about 7 years since James Heathers and I first started investigating his work, Guéguen has started publishing again! With co-authors, to be sure (almost all of our critiques so far have been of his solo-authored papers, which makes things less messy), but nevertheless, he's back in business. Will it be a solid registered report with open data, fit for the brave new post-train wreck world, or will it be more Benny Hill Science™? Let's take a look:

Martini, A., Guéguen, N., Jacob, C., & Fischer-Lokou, J. (2024). Incidental similarity and influence of food preferences and judgment: Changing to be closer to similar people. European Journal of Public Health Studies, 7(2), 1-10. https://doi.org/10.46827/ejphs.v7i2.176

On 2024-08-08 I was able to download the article from here.

I think it's fair to say that the European Journal of Public Health Studies is not what most people would regard as a top-drawer journal. It does not appear to be indexed in Scopus or PubMed and its website is rather modest. On the other hand, its article processing charge is just $85, which is hard to argue with, and of course it's what's in the paper that counts.

The study involved finding ways to get children to eat more fruits and/or vegetables, which may ring a few bells. I'll let you read the paper to see what each variable means, but basically, children aged 8 or 9 were asked a number of questions on a 1–7 scale about how much they liked, or were likely to consume, fruits or vegetables after a brief intervention (i.e., having an adult talk to the child about their own childhood food preferences — the "Similarity" condition — or not).

Let's have a look at the results. Here is Table 2:

First, note that although the sample size was originally reported as 51 (25 Similarity, 26 Control), and the t tests in Table 1 reflect that with their 49 degrees of freedom, here we have df=48. Visual inspection of the means (you can do GRIM in your head with sufficiently regular numbers), backed up with some calculation because I am getting old, suggests that the only possibility that is consistent with the reported means is that one participant is missing from the control condition, so we can continue on the basis that N=25 in each condition.

There is quite a ceiling effect going on in the Similarity condition. Perhaps this is not unreasonable; these are numbers reported on a 1–7 scale by children, who are presumably mostly eager to help the researcher and might well answer 7 on a social-desirability basis (a factor that the authors do not seem to have taken into account, at least as far as one can tell from reading their "limitations" paragraph). I set out to use SPRITE to see what the pattern of likely individual responses might be, and that was where the fun started. For both "Pleasure to respond" and "Feeling understood by the instructor", SPRITE finds no solution. I also attempted to generate a solution manually for each of those variables, but without success. (If you want to try it yourself, use this spreadsheet. I would love to know if you can get both pink cells to turn green.)

Thus, we have not one but two examples of that rarest of things, a GRIMMER inconsistency, in the same paper. I haven't been this excited since 2016. (OK, GRIMMEST is probably even rarer, although we do have at least one case, also from Guéguen, and I seem to vaguely remember that Brian Wansink may have had one too).

I am about to go on vacation, but when I return I hope to blog about another recent paper from the same author, this time featuring (drum roll please) RIVETS, which I like to think of as the Inverted Jenny of error detection.

Attack of the 50 foot research assistants: Lee et al. (2019), Study 3

This post is about some issues in Study 3 of the following article:

 Lee, J. J., Hardin, A. E., Parmar, B., & Gino, F. (2019). The interpersonal costs of dishonesty: How dishonest behavior reduces individuals' ability to read others' emotions. Journal of Experimental Psychology: General, 148(9), 1557–1574. https://doi.org/10.1037/xge0000639

On 2023-11-06 I was able to download the article from here.

This article is paper #29 in the Many Co-Authors project, where researchers who have co-authored papers with Professor Francesca Gino are reporting the provenance of the data in those papers, following the discovery of problems with the data in four articles co-authored by Professor Gino.

 

In the tables on the Many Co-Authors page for paper #29, two of the three co-authors of this article have so far (2023-11-10) provided information about the provenance of the data for this article, with both indicating that Professor Gino was involved in the data collection for Study 3. This note from Julia Lee Cunningham, the lead author, provides further confirmation:

For Study 3, Gino’s research assistant ran the laboratory study at Harvard Business School Research Lab for the partial data on Gino’s Qualtrics account. The co-authors have access to the raw data and were able to reproduce the key published results for Study 3.

In this study, pairs of participants interacted by telling each other stories. In one condition ("dishonest"), one member of the pair (A) told a fake story and the other (B) told a true story. In the other condition ("honest"), both members of the pair told true stories. Then, B evaluated their emotions during the exercise, and A evaluated their perceptions of B's emotions. The dependent variable ("emotional accuracy") was the ability of A to accurately evaluate how B had been feeling during the exercise. The results showed that when A had been dishonest (by telling a fake story), they were less accurate in their evaluation of B's emotional state.

 

The dataset for Study 3 is available as part of the OSF repository for the whole article here. It consists of an SPSS data file (.SAV) and a "syntax" (code) file (.SPS). I do not currently have an SPSS licence, so I was unable to run the code, but it seems to be fairly straightforward, running the focal t test from the study followed by the ANCOVAs to test whether gender moderated the relationship between condition and emotional accuracy.

 

I converted the dataset file to .CSV format in R and was then able to replicate the focal result of the study ("participants in the dishonest condition (M = 1.58, SD = 0.63) were significantly less
accurate at detecting others’ mental and affective states than those in the honest condition (M=1.39, SD = 0.54), t(209) = 2.37, p = .019", p. 1564, emphasis in original). My R code gave me this result:

> t.test(df.repl.dis$EmoAcc, df.repl.hon$EmoAcc, var.equal=TRUE)

	Two Sample t-test

data:  df.repl.dis$EmoAcc and df.repl.hon$EmoAcc
t = 2.369, df = 209, p-value = 0.01875

However, this is not the whole story. Although the dataset contains records from 250 pairs of participants, the article states (p. 1564):

 

As determined by research assistants monitoring each session, pairs were excluded for the following reasons: the wrong partner told their story first; they asked so many questions during the session that it became apparent they were not actually reading their survey instructions or questions (e.g., “What story am I supposed to be telling?”); or they were actively on their phone during the storytelling portion of the session. Exclusions were due to the actions of either individual in the pair; thus, of the 500 individuals, 39 did not follow instructions. This resulted in 106 pairs in the dishonest condition and 105 pairs in the honest condition.

The final total of 211 pairs is confirmed by the 209 degrees of freedom of the above t test.

Conveniently, the results for the 39 excluded pairs are available in the dataset. They are excluded from analysis based on a variable named "Exclude_LabNotes" (although sadly, despite this name, the OSF data repository does not contain any lab notes that might explain the basis on which each exclusion was made). It is thus possible to run the analyses on the full dataset of 250 pairs, with no exclusions. When I did that, I obtained this result:

> t.test(df.full.dis$EmoAcc, df.full.hon$EmoAcc, var.equal=TRUE)

	Two Sample t-test

data:  df.full.dis$EmoAcc and df.full.hon$EmoAcc
t = 0.20148, df = 246, p-value = 0.8405

(Alert readers may notice that the degrees of freedom for this independent t test are only 246 rather than the expected 248. On inspection of the dataset, it appears that one record has NA for experimental condition and another has NA for emotional accuracy. Both of these records were also manually excluded by the research assistants, but they could not have been used in any of the t tests anyway. Hence, it seems fairer to say that 37 out of 248 participant pairs, rather than 39 out of 250, were excluded based on notes made by the RAs.)

 

As you can see, there is quite a difference from the previous t test (p = 0.8405 versus p = 0.01875). Had these 37 participant pairs not been excluded, there would be no difference between the conditions; put another way, the exclusions drive the entire effect. I ran the same t test on (only) these excluded participants:

> t.test(df.dis$EmoAcc, df.hon$EmoAcc, var.equal=TRUE)

	Two Sample t-test

data:  df.exconly.dis$EmoAcc and df.exconly.hon$EmoAcc
t = -4.1645, df = 35, p-value = 0.0001935

Cohen's d for this test is 1.412, which is a very large effect indeed among people who are not paying attention.

 

I think it is worth illustrating these results graphically. First, a summary of the three t tests:

Second, an illustration of where each observation was dropped from its respective per-condition sample:

[[Edit 2023-11-11 19:05 UTC: I updated the second figure above. The previous version reported "t(34) = 4.56", reflecting a t test with equal variances not assumed in which the calculated degrees of freedom were 34.466. This is actually the more correct way to calculate the t statistic, but I have been using "equal variances assumed" in all of the other analyses in this post for compatibility with the original article, which used analyses from SPSS in which the assumption of equal variances is the default. See also this article. ]]

 

This is quite remarkable. One might imagine that participants who were not paying attention to the instructions, or goofing off on their phones, would, overall, give responses that would show no effect, because their individual responses would have been noisy and/or because the set of excluded participants was approximately balanced across conditions (and there is no difference between the conditions for the full sample). Indeed, a legitimate reason to exclude these participants would be that their results are likely to be uninformative noise and so, if they were numerous enough, their inclusion might lead to a Type II error. But instead, it seems that these excluded participants showed a very strong effect in the opposite direction to the hypothesis (as shown by the negative t statistic). That is, if these results are to be believed, something about the fact that either A or B was not following the study instructions made A much better (or less bad) at determining B's emotions when telling a fake (versus true) story. There were 14 excluded participant pairs in the "dishonest" condition, with a mean emotional accuracy score (lower = more accurate) for A of 1.143, and 23 in the "honest" condition, with a mean emotional accuracy score of 2.076; for comparison, the mean score for the full sample across both conditions is 1.523.

I hope the reader will forgive me for saying that this explanation does not seem very likely — and if it were true, it would presumably be the basis of intense interest among psychologists. Rather, there seem to be two other plausible explanations (but feel free to point out any others that you can think of in the comments). One is that the extreme results of the excluded participants arose by chance — and, hence, the apparent effect in favour of the authors' hypothesis caused by their exclusion was also the result of chance. The other, painful though it is to contemplate, is that the research assistants may have excluded participants in order to give a result in line with the hypotheses.

 

I simulated how likely it would be for the removal of 37 random participant pairs from the sample of 248 complete records to give a statistically significant result. I ran 1,000,000 simulations and obtained only 12 p values less than 0.05 for the t test on the resulting sample of 211 pairs. The smallest p value that I obtained was 0.03387, which is higher than the one reported in the article. To put it another way, out of a million attempts I was unable to obtain even one result as extreme as the published one by chance.

Now, this process can surely be subjected to some degree of criticism from a statistical inference point of view. After all, if the report in the article is correct, the excluded participants were not selected truly at random, and they might differ in other ways from the rest of the sample, with those differences perhaps interacting with the experimental condition. There might be other, more formally correct ways to test the idea that the exclusions of participant pairs were independent of their scores. However, as mentioned earlier, I do not think that it can be seriously argued that there was some extremely powerful psychological process, contrary to the study hypothesis, taking place specifically with the excluded participants.

So it seems to me that, by elimination, the most plausible remaining explanation is that the research assistants selected which participants to exclude based on their scores, in such a way as to produce results that favoured the authors' hypothesis. Exactly how they were able to do that, given that those scores were only available in Qualtrics, when their job was (presumably) to help participants sitting in the laboratory to understand the process and to check who was spending time on their phone, is unclear to me, but doubtless there is a coherent explanation. Indeed, Professor Gino has already suggested (see point 274 here) that research assistants may have been responsible for perceived anomalies in other studies on which she was an author, although so far no details on how exactly this might have happened have been made public. I hope that she will be able to track down the RAs in this case and establish the truth of the matter with them.

Supporting files

I have made my analysis code available here. I encourage you to use the authors' original SPSS data file from the OSF link given above, and convert it to CSV format using the commented-out line at the top of the script. However, as a convenience, I have made a copy of that CSV file available along with my code.

 

Acknowledgements

I thank Daniël Lakens and two anonymous readers of earlier drafts of this post for their comments. One of those people also kindly provided the two charts in the post.

 

I wrote to Julia Lee Cunningham to give her a heads up about this post. With her permission, I will quote any reply that she might make here.

Data errors in Mo et al.'s (2023) analysis of wind speed and voting patterns

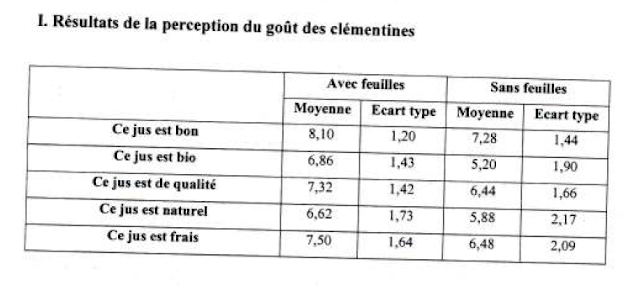
This post is about some issues in the following article, and most notably its dataset:

Mo, C. H., Jachimowicz, J. M., Menges, J. I., & Galinsky, A. D. (2023). The impact of incidental environmental factors on vote choice: Wind speed is related to more prevention‑focused voting. Political Behavior. Advance online publication. https://doi.org/10.1007/s11109-023-09865-y

You can download the article from here, the Supplementary Information from here [.docx], and the dataset from here. Credit is due to the authors for making their data available so that others can check their work.

Introduction

The premise of this article, which was brought to my attention in a direct message by a Twitter user, is that the wind speed observed on the day of an "election" (although in fact, all the cases studied by the authors were referendums) affects the behaviour of voters, but only if the question on the ballot represents a choice between prevention- and promotion-focused options, in the sense of regulatory focus theory. The authors stated in their abstract that "we find that individuals exposed to higher wind speeds become more prevention-focused and more likely to support prevention-focused electoral options".

This article (specifically the part that focused on the UK's referendum on leaving the European Union ("Brexit") has already been critiqued by Erik Gahner here.

I should state from the outset that I was skeptical about this article when I read the abstract, and things did not get better when I found a couple of basic factual errors in the descriptions of the Brexit referendum:

1. On p. 9 the authors claim that "The referendum for UK to leave the European Union (EU) was advanced by the Conservative Party, one of the three largest parties in the UK", and again, on p. 12, they state "In the case of the Brexit vote, the Conservative Party advanced the campaign for the UK to leave the EU". However, this is completely incorrect. The Conservative Party was split over how to vote, but the majority of its members of parliament, including David Cameron, the party leader and Prime Minister, campaigned for a Remain vote (source).
2. At several points, the authors claim that the question posed in the Brexit referendum required a "Yes"/"No" answer. On p. 7 we read "For Brexit, the “No” option advanced by the Stronger In campaign was seen as clearly prevention-oriented ... whereas the “Yes” option put forward by the Vote Leave campaign was viewed as promotion-focused". The reports of result coding on p. 8, and the note to Table 1 on p. 10, repeat this claim. But this is again entirely incorrect. The options given to voters were to "Remain" (in the EU) or "Leave" (the EU). As the authors themselves note, the official campaign against EU membership was named "Vote Leave" (and there was also an unofficial campaign named "Leave.EU"). Indeed, this choice was adopted, rather than "Yes" or "No" responses to the question "Should the United Kingdom remain a member of the European Union?", precisely to avoid any perception of "positivity bias" in favour of a "Yes" vote (source). Note also here that, had this change not been made, the pro-EU vote would have been "Yes", and not the (prevention-focused) "No" claimed by the authors. (*)

Nevertheless, the article's claims are substantial, with remarkable implications for politics if they were to be confirmed. So I downloaded the data and code and tried to reproduce the results. Most of the analysis was done in Stata, which I don't have access to, but I saw that there was an R script to generate Figure 2 of the study that analysed the Swiss referendum results, so I ran that.

My reproduction of the original Figure 2 from the article. The regression coefficient for the line in the "Regulatory Focus Difference" condition is B=0.545 (p=0.00006), suggesting that every 1km/h increase in wind speed produces an increase of more than half a percentage point in the vote for the prevention-oriented campaign.

Catastrophic data problems

I had no problem in reproducing Figure 2 from the article. However, when I looked a little closer at the dataset (**) I noticed a big problem in the numbers. Take a look at the "DewPoint" and "Humidity" variables for "Election 50", which corresponds to Referendum 24 (***) in the Supplementary Information, and see if you can spot the problem.

Neither of those variables can possibly be correct for "Election 50" (note that the same issues affect the records for every "State", i.e., Swiss canton):

• DewPoint, which would normally be a Fahrenheit temperature a few degrees below the actual air temperature, contains numbers between 0.401 and 0.626. The air temperature ranges from 45.3 to 66.7 degrees. For the dew point temperatures to be correct would require the relative humidity to be around 10% (calculator), which seems unlikely in Switzerland on a mild day in May. Perhaps these DewPoint values in fact correspond to the relative humidity?
• Humidity (i.e., relative atmospheric humidity), which by definition should be a fraction between 0 and 1, is instead a number in the range from 1008.2 to 1015.7. I am not quite sure what might have caused this. These numbers look like they could represent some measure of atmospheric pressure, but they only correlate at 0.538 with the "Pressure" variable for "Election 50".

To evaluate the impact of these strange numbers on the authors' model, I modified their R script, Swiss_Analysis.R, to remove the records for "Election 50" and obtained this result from the remaining 23 referendums:

Figure 2 with "Election 50" (aka Referendum 24) removed from the model.

The angle of the regression line on the right is considerably less jaunty in this version of Figure 2. The coefficient has gone from B=0.545 (SE=0.120, p=0.000006) to B=0.266 (SE=0.114, p=0.02), simply by removing the damaged data that were apparently causing havoc with the model.

How robust is the model now?

A p value of 0.02 does not seem like an especially strong result. To test this, after removing the damaged data for "Election 50", I iterated over the dataset removing a further different single "Election" each time. In seven cases (removing "Election" 33, 36, 39, 40, 42, 46, or 47) the coefficient for the interaction in the resulting model had a p value above the conventional significance level of 0.05. In the most extreme case, removing "Election 40" (i.e., Referendum 14, "Mindestumwandlungsgesetz") caused the coefficient for the interaction to drop to 0.153 (SE=0.215, p=0.478), as shown in the next figure. It seems to me that if the statistical significance of an effect disappears with the omission of just one of the 23 (****) valid data points in 30% of the possible cases, this could indicate a lack of robustness in the effect.

Figure 2 with "Election 50" (aka Referendum 24) and "Election 40" (aka Referendum 14) removed from the model.

Other issues

Temperature precision

The ambient temperatures on the days of the referendums (variable "Temp") are reported with eight decimal places. It is not clear where this (apparently spurious) precision could have come from. Judging from their range the temperatures would appear to be in degrees Fahrenheit, whereas one would expect the original Swiss meteorological data to be expressed in degrees Celsius. However, the conversion between the two scales is simple (F = C * 1.8 + 32) and cannot introduce more than one extra decimal place. The authors state that "Weather data were collected from www.forecast.io/raw/", but unfortunately that link redirects to a page that suggests that this source is no longer available.

Cloud cover

The "CloudCover" variable takes only eight distinct values across the entire dataset, namely 2, 3, 5, 6, 8, 24, 34, and 38. It is not clear what these values represent, but it seems unlikely that they (all) correspond to a percentage or fraction of the sky covered by clouds. Yet, this variable is included in the regression models as a linear predictor. If the values represent some kind of ordinal or even nominal coding scheme, rather than being a parameter of some meteorological process, then including this variable could have arbitrary consequences for the regression (after all, 24, 34, and 38 might equally well have been coded ordinally as 9, 10, and 11, or perhaps nominally as -99, -45, and 756). If the intention is for these numbers to represent obscured eighths of the sky ("oktas"), then there is clearly a problem with the values above 8, which constitute 218 of the 624 records in the dataset (34.9%).

Income

It would also be interesting to know the source of the "Income" data for each Swiss canton, and what this variable represents (e.g., median salary, household income, gross regional product, etc). After extracting the income data and canton numbers, and converting the latter into names, I consulted several Swiss or Swiss-based colleagues, who expressed skepticism that the cantons of Schwyz, Glarus, and Jura would have the #1, #3, and #4 incomes by any measure. I am slightly concerned that there may have been an issue with the sorting of the cantons when the Income variable was populated. The Supplementary Information says "Voting and socioeconomic information was obtained from the Swiss Federal Office of Statistics (Bundesamt für Statistik 2015)", and that reference points to a web page entitled “Detaillierte Ergebnisse Der Eidgenössischen Volksabstimmungen” with URL http://www.bfs.admin.ch/bfs/portal/de/index/themen/17/03/blank/data/01.html, but that link is dead (and in any case, the title means "Detailed results of Federal referendums"; such a page would generally not be expected to contain socioeconomic data).

Swiss cantons (using the "constitution order" mapping from numbers to names) and their associated "Income", presumably an annual figure in Swiss francs. Columns "Income(Mo)" and the corresponding rank order "IncRank" are from Mo et al.'s dataset; "Statista" and "StatRank" are from statista.com.

I obtained some fairly recent Swiss canton-level household income data from here and compared it with the data from the article. The results are shown in the figure above. The Pearson correlation between the two sets of numbers was 0.311, with the rank-order correlation being 0.093. I think something may have gone quite badly wrong here.

Turnout

The value of the "Turnout" variable is the same for all cantons. This suggests that the authors may have used some national measure of turnout here. I am not sure how much value such a variable can add. The authors note (footnote 12, p. 17) that "We found that, except for one instance, no other weather indicator was correlated with the number of prevention-focused votes without simultaneously also affecting turnout rates. Temperature was an exception, as increased temperature was weakly correlated with a decrease in prevention-focused vote and not correlated with turnout". It is not clear to me what the meaning would be of calculating a correlation between canton-level temperature and national-level turnout.

Voting results do not always sum to 1

Another minor point about whatever cleaning has been performed on the dataset is that in 68 out of 624 cases (10.9%), the sum of "VotingResult1" and "VotingResult2" — representing the "Yes" and "No" votes — is 1.01 and not 1.00. Perhaps this is the result of the second number being generated by the first being subtracted from 1.00 when the first number was expressed as a percentage with one decimal place, with both numbers subsequently being rounded and something ambiguous happening with the last digit 5. In any case, it would seem important for these two numbers to sum to 1.00. This might not make an enormous amount of difference to the results, but it does suggest that the preparation of the data file may not have been done with excessive care.

Mean-centred variables

Two of the control variables, "Pressure" and "CloudCover", appear in the dataset in two versions, raw and mean-centred. There doesn't seem to be any reason to mean-centre these variables, but it is something that is commonly done when calculating interaction terms. I wonder whether at some point in the analyses the authors tested atmospheric pressure and cloud cover, rather than wind speed, as possible drivers of an effect on voting. Certainly there seems to be quite a lot of scope for the authors to have wandered around Andrew Gelman's "Garden of forking paths" in these analyses, which do not appear to have been pre-registered.

No measure of population

Finally, a huge (to me, anyway) limitation of this study is that there is no measure of, or attempt to weight the results by, the population of the cantons. The most populous Swiss canton (Zürich) has a population about 90 times that of the least populous (Appenzell Innerrhoden), yet the cantons all have equal weight in the models. The authors barely mention this as a limitation; they only mention the word "population" once, in the context of determining the average wind speed in Study 1. Of course, the ecological fallacy [.pdf] is always lurking whenever authors try to draw conclusions about the behaviour of individuals, whether or not the population density is taken into account, although this did not stop the authors from claiming in their abstract that "we find that individuals [emphasis added] exposed to higher wind speeds become more prevention-focused and more likely to support prevention-focused electoral options", or (on p. 4) stating that "We ... tested whether higher wind speed increased individual’s [punctuation sic; emphasis added] prevention focus".

Conclusion

I wrote this post principally to draw attention to the obviously damaging errors in the records for "Election 50" in the Swiss data file. I have also written to the authors to report those issues, because these are clearly in need of urgent correction. Until that has happened, and perhaps until someone else (with access to Stata) has conducted a re-analysis of the results for both the "Swiss" and "Brexit/Scotland" studies, I think that caution should be exercised before citing this paper. The other issues that I have raised in this post are, of course, open to critique regarding their importance or relevance. For the avoidance of doubt, given the nature of some of the other posts that I have made on this blog, I am not suggesting that anything untoward has taken place here, other than perhaps a degree of carelessness.

Supporting files

I have made my modified version of Mo et al.'s code to reproduce Figure 2 available here, in the file "(Nick) Swiss_Analysis.R". If you decide to run it, I encourage you to use the authors' original data file ("Swiss.dta") from the ZIP file that can be downloaded from the link at the top of this post. However, as a convenience, I have made a copy of this file available along with my code. In the same place you will also find a small Excel table ("Cantons.xls") containing data for my analysis of the canton-level income question.

Acknowledgements

Thanks to Jean-Claude Fox for doing some further digging on the Swiss income numbers after this post was first published.

Footnotes

(*) Interestingly, the title of Table 1 and, even more explicitly, the footnote on p. 10 ("Remain" with an uppercase initial letter) suggest that the authors may have been aware that the actual voting choices were "Remain" and "Leave". Perhaps these were simplified to "No" and "Yes", respectively, for consistency with the reports of the Scottish independence referendum; but if so, this should have been reported.

(**) I exported the dataset from Stata's .dta format to .csv format using rio::convert(). I also confirmed that the errors that I report in this post were present in the Stata file by inspecting the data structure after the Stata file had been read in to R.

(***) The authors coded the Swiss referendums, which are listed with numbers 1–24 in the Supplementary Information, as 27–50, by adding 26. They also coded the 26 cantons of Switzerland as 51–76, apparently by adding 50 to the constitutional order number (1 = Zürich, 26 = Jura; see here), perhaps to ensure that no small integer that might creep into the data would be seen as either a valid referendum or canton (a good practice in general). I was able to check that the numerical order of the "State" variable is indeed the same as the constitutional order by examining the provided latitude and longitude for each canton on Google Maps (e.g., "State" 67, corresponding to the canton of St Gallen with constitutional order 17, has reported coordinates of 47.424482, 9.376717, which are in the centre of the town of St Gallen).

(****) I am not sure whether a single referendum in 26 cantons represents 1 or 26 data points. The results from one canton to the next are clearly not independent. I suppose I could have written "4.3% of the data" here.

Strange numbers in the dataset of Zhang, Gino, & Norton (2016)

In this post I'm going to be discussing this article:

Zhang, T., Gino, F., & Norton, M. I. (2016). The surprising effectiveness of hostile mediators. Management Science, 63(6), 1972–1992. https://doi.org/10.1287/mnsc.2016.2431

 

You can download the article from here and the dataset from here.

[[ Begin update 2023-07-03 16:12 UTC ]]

Following feedback from several sources, I now see how it is in fact possible that these data could have been the result of using a slider to report the amount of money being requested. I still think that this would be a terrible way to design a study (see my previous update, below), as it causes a loss of precision for no obvious good reason compared to having participants type a maximum of 6 digits, and indeed the input method is not reported in the article. However, if a slider was used, then with multiple platforms the observed variety of data could have arisen.

 

In the interests of transparency I will leave this post up, but with the caveat that readers should apply caution in interpreting it until we learn the truth from the various inquiries and resolution exercises that are ongoing in the Gino case.

[[ End update 2023-07-03 16:12 UTC ]]

The focus of my interest here is Study 5. Participants (MTurk workers) were asked to imagine that they were a carpenter who had been given a contract to furnish a number of houses, but decided to use better materials than had been specified and so had overspent the budget by $300,000. The contractor did not want to reimburse them for this. The participants were presented with interactions that represented a mediation process (in the social sense of the word "mediation", not the statistical one) between the carpenter and the contractor. The mediator's interactions were portrayed as "Nice", "Bilateral hostile" (nasty to both parties), or "Unilateral hostile" (nasty to the carpenter only). After this exercise, the participants were asked to say how much of the $300,000 they would ask from the contractor. This was the dependent variable to show how effective the different forms of mediation were.

The authors reported (p. 1986):

We conducted a between-subjects ANOVA using participants’ demands from their counterpart as the dependent variable. This analysis revealed a significant effect for mediator’s level and directedness of hostility, F(2, 134) = 6.86, p < 0.001, partial eta² = 0.09. Post hoc tests using LSD corrections indicated that participants in the bilateral hostile mediator condition demanded less from their counterpart (M = $149,457, SD = 65,642) compared with participants in the unilateral hostile mediator condition (M = $208,807, SD = 74,379, p < 0.001) and the nice mediator condition (M = $183,567, SD = 85,616, p = 0.04). The difference between the latter two conditions was not significant (p = 0.11).

Now, imagine that you are a participant in this study. You are being paid $1.50 to pretend to be someone who feels that they are owed $300,000. How much are you going to ask for? I'm guessing you might ask for all $300,000; or perhaps you are prepared to compromise and ask for $200,000; or you might split the difference and ask for $150,000; or you might be in a hurry and think that 0 is the quickest number to type.

Let's look at what the participants actually entered. In this table, each cell is one participant; I have arranged them in columns, with each column being a condition, and sorted the values in ascending order.

 

This makes absolutely no sense. Not only did 95 out of 139 participants choose a number that wasn't a multiple of $1,000, but also, they chose remarkably similar non-round numbers. Twelve participants chose to ask for exactly $150,323 (and four others asked for $10,323, $170,323, or $250,323). Sixteen participants asked for exactly $150,324. Ten asked for $149,676, which interestingly is equal to $300,000 minus the aforementioned $150,324. There are several other six-digit, non-round numbers that occur multiple times in the data. Remember, every number in this table represents the response of an independent MTurk worker, taking the survey in different locations across the United States.

To coin a phrase, it is not clear how these numbers could have arisen as a result of a natural process. If the authors can explain it, that would be great.

[[ Begin update 2023-07-02 12:38 UTC ]]

Several people have asked, on Twitter and in the comments here, whether these numbers could be explained by a slider having been used, instead of a numerical input field. I don't think so, for several reasons:

1. It makes no sense to use a slider to ask people to indicate a dollar amount. It's a number. The authors report the mean amount to the nearest dollar. They are, ostensibly at least, interested in capturing the precise dollar amount.
2. Had the authors used a slider, they would presumably have done so for a very specific reason, which one would imagine they would have reported.
3. Some of the values reported are 153,023, 153,024, 150,647, 150,972, 151,592, and 151,620. The differences between these values are 1, 323, 325, 620, and 28. In another sequence, we see 180,130, 180,388, and 180,778, separated by 258 and 390; and in another, 200,216, 200,431, 200,864, and 201,290, separated by 215, 433, and 426. Even if we assume that the difference of 1 is a rounding error, in order for a slider to have the granularity to be able to indicate all of those numbers while also covering the range from 0 to 300,000, it would have to be many thousands of pixels wide. Real-world on-screen sliders typically run from 0 to 100 or 0 to 1000, with each of 400 or 500 pixels representing perhaps 0.20% or 0.25% of the available range.

Of course, all of this could be checked if someone had access to the original Qualtrics account. Perhaps Harvard will investigate this paper too...

[[ End update 2023-07-02 12:38 UTC ]]

 

Acknowledgements

Thanks to James Heathers for useful discussions, and to Economist 1268 at econjobrumors.com for suggesting that this article might be worth looking at.